本文由 发布，转载请注明出处，如有问题请联系我们！ 发布时间: 2021-08-01斐波那契数列时间复杂度推导-解析西斐波那契数列通项公式

宣布工作中3年了，想写更雅致的编码。

因此之前一直在刷leetcode，填补算法设计和优化算法层面的专业知识。

尽管我还在院校学过，但我只有一个大约的掌握。仅有通过两年的具体工作中，大家才会搞清楚算法设计和优化算法的必要性。

如果你是通信专业或硬件技术专业的，你一定了解我们可以从时域频域剖析一个数据信号。

那麼怎样剖析电子信息科学或开发软件中的计算方法呢？考量好坏有两个层面:算法复杂度和空中间的复杂性。

算法复杂度：实行当今优化算法所耗费的’時间’。空间复杂度：实行当今优化算法所占有的运行内存。

在这篇博闻中，大家来剖析一下算法复杂度。

算法复杂度真的是测算’時间’吗？算法复杂度公式计算：大O标记表达方式普遍算法复杂度种类及编码剖析参量型O(1)多数型O(log n)线性型O(n)线形多数型O(n log n)平方米型O(n^2).立方米型O(n^3).K三次方型O(n^k)平方米底指数型O(2^n).立方米底指数型O(3^n).K次底指数型O(k^n)阶乘型O(n!)怎样看待斐波那契数列的算法复杂度O(2^N)?怎样看待阶乘型算法复杂度O(n!)？参考文献

算法复杂度真的是在预估‘時间’吗？

把提示的实施時间想像成算法复杂度？

这类形式是最形象化最非常容易想起的。

可是有一个难题，便是当编码在不一样特性.不一样情况的设备上运作时，会主要表现出彻底不一样的运转時间。例如我有一个32GB存储空间的mbp和一个8GB的台式电脑，假定别的硬件配置标准如cpu.电脑主板和设备负荷情况一致。一般32GB运行内存比8GB运行内存运作更快。并且，这类仅有单一因素的梦想情况也难以完成。

因而，不太可能将优化算法耗费的计算时间为算法复杂度。

在“時间”的多元性中，大家常说的“時间”究竟指的是什么？

聪慧的老前辈想起了一个方法:大o注释。

大表明中有一个比较复杂的计算能力逻辑性。如果我们懒，不证实公式计算，用好啦会很厉害。

为什么不证实或是再做一次？我大一的情况下以前上过一门叫高等代数的课。有一个题型叫:请证实1 1=2。

见到这种题型，你应该知道为什么不细究大O标记身后的数学课。

算法复杂度公式计算:大o标记。

T(n) = O(f(n))f(n)就是指每排程序执行频次之和f(n)能够是这种值：1，log n，n，nlog n，n^2，n^3，n^k，2^n，n!f(n)与O成正比O(f(n))能够是这种值：O(1)，O(log n)，O(n)，O(nlog n)，O(n^2)，O(n^3)，O(n^k)，O(2^n)，O(n!)大O表达方式具体表明的是程序执行時间的提高趋势分析，并不是实际的运转時间，是一种发展趋势预计大O表达方式中的f(n)是自然数。许多情况下不容易根本是1，log n，n，nlog n，n^2，n^3，n^k，2^n，n!这种详细的值。比如斐波那契数列的真正算法复杂度为O(2^N-1)，因为N->∞，因此能够类似为O(2^N)。

有关斐波那契数列算法复杂度的大量剖析，请看下面:怎样看待斐波那契数列的算法复杂度o (2 n)？

普遍的算法复杂度种类和编码剖析。

早已谈了许多基础理论，现在是时候给我看看编码了。使我们从一个大的复杂性图逐渐。

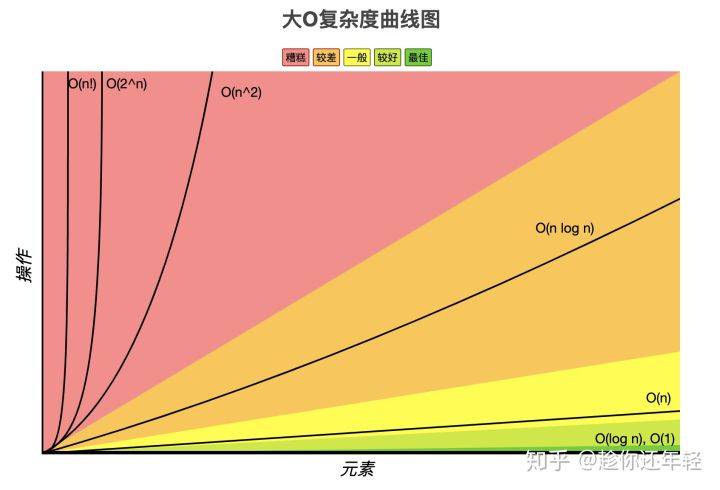下边的算法复杂度依照最好是->好->一般->差->差的排列顺序。

参量型O(1)多数型O(log n)线性型O(n)线形多数型O(n log n)平方米型O(n^2).立方米型O(n^3).K三次方型O(n^k)平方米底指数型O(2^n).立方米底指数型O(3^n).K次底指数型O(k^n)阶乘型O(n!)

O型(1)

多见于取值和引入等简单实际操作优化算法耗费不随自变量提高而提高，特性最好不管程序执行是多少行，即便有几千几万行，算法复杂度都为O(1)具体开发设计流程中，一次递归算法的算法复杂度也为O(1)。由于O(1^n)不管n为很多都为O(1)let i = 0;let j = 9;i ;j--;let k = i j;

编码剖析:I为1，j为10，k为11。算法复杂度为0(1)。

多数型0(多数n)

常见程序执行频次为x，n为总体目标数据。合乎2^x=n，推论出x=log2(n)（log n）的状况优化算法耗费随n的提高而提高，特性不错let n = 100;let i = 1;while(i

编码剖析:我是128。n为100，算法复杂度为O(log2(100))。由于Math.log2(100)≈6.64，因此最后的算法复杂度是O(6.65)。

O型(n)

多见于一次for循环，while循环系统优化算法耗费随n的提高而提高，特性一般不管n值有多大，即便是Inifinity，算法复杂度都为O(n)let n = 100;let j = 0;for(let i = 0;i

编码剖析:I为100，j为99。n为100，算法复杂度为O(100)。

多数O型(多数n)

常见于一个对算法复杂度为O(log2(n))的程序执行一个n次循环系统优化算法耗费随n的提高而提高，特性较弱let n = 100;for(let m = 0; m

编码剖析:我是128。m为100，n为100，算法复杂度为O(m log2(n))。由于100* Math.log2(100)≈664.39，因此最后的算法复杂度为O(664.39)。

o型(n 2)，o型(n 3)，o型(n k)。

最普遍的优化算法算法复杂度，可用以快速开发领域模型多见于2次for循环，或是3次for循环，及其k次for循环优化算法耗费随n的提高而提高，特性槽糕具体开发设计流程中，不建议应用K值过大的循环系统，不然编码将十分无法维护保养let n = 100let v = 0;for(let i =0;i

编码剖析:v为990000，I为100，j为100，n为100，算法复杂度为o(100 ^ 2)。那便是O(10000)。

三次O(n ^ 3)和K次O(n ^ K)类似平方米O(n ^ 2)，仅仅多了好多个循环系统。

// 立方米型O(n^3)for(let i =0;i

方底(2 n)的指数型o，立方米底(3 n)的指数型o，k倍底(k ^ n)的指数型o。

多见于2次递归算法的状况，3次递归算法及其k次递归算法的状况优化算法耗费随n的提高而提高，特性槽糕具体开发设计流程中，k为1时，一次递归算法的算法复杂度为O(1)。由于O(1^n)不管n为很多都为O(1)。

斐波那契数列(兔子数列，黄金分割数列):1，1，2，3，5，8，13，21，34文章标题:leetcode 509斐波那契数。

解决方法:509。斐波那契数。

/** * @param {number} N * @return {number} */var fib = function (N) { /** * 打法1: 递归算法 * 特性: 88ms 34.2MB * 算法复杂度：O(2^N) */ if (N

假定n相当于100。编码剖析:結果是xxx。由于电脑浏览器立即卡住了。它也不可在nodejs中运作。实际缘故是2的100三次方确实太大。数不回来。n为100，算法复杂度为o (2 100)。由于math.pow (2，100) = 1.2676506002282294e 30，因此最后的算法复杂度为o (1.267650602282294e 30)。大到超乎想象。

三次指数型O (3 n)和第k次指数型O (k n)与平方米指数型O (2 n)类似，仅仅数量改成3和k。

O(Math.pow(3, n))O(Math.pow(k, n))

假定n是100，k是5。Math.pow(3，n)是5.153775207320113e 47。Math.pow(5，n)是7.888609052210118e 69。算法复杂度也非常高，真的是指数级的发生爆炸。

有关斐波那契数列的算法复杂度o (2 n)的大量剖析，请看下面:怎样看待斐波那契数列的算法复杂度o (2 n)？

阶乘种类O(n！)

极为不普遍优化算法耗费随n的提高而提高，特性槽糕function nFacRuntimeFunc(n) { for(let i=0; i

阶乘种类O(n！)依据(n！ (n-1)！ (n-2)！ 1) ((n-1)！ (n-2)！ 1) ...计算方式。哦，这也是多种阶乘的和。不仅是n * (n-1) * (n-2) * (n-3) 1。假定n从0到10，其时间复杂度为O(n！)先后是1.4.15.64.325.1956.13699.109600.986409.9864100……为了更好地和上边别的优化算法的复杂性开展较为，n为100时的数据多少钱？o (2 n)为10时为1024，n为100时o (2 n)立即电脑浏览器被卡死。O(n！)仅有10就贴近1000万，假如n设定为100，就没法计算机器点燃时的标值。因而，当n为100时，O(n！别想想，这是一个恐怖的极大数据。

阶乘算法复杂度O(n！)能够在下面寻找:怎样看待阶乘算法O(n！)?

怎样看待斐波那契数列的算法复杂度o (2 n)？

O(2^N)Math.pow(base, ex)，2个递归算法因此base是2。N得话是由于N->∞，但实际上真真正正是O(2^(N-1))。/** * @param {number} N * @return {number} */var fib = function (N) { /** * 打法1: 递归算法 * 特性: 88ms 34.2MB */ console.log('foo'); if (N

印刷字体的总数是o(2n)11o(2 0)22 1 1o(2 1)32 2 1o(2 2)42 3 1o(2 3)52 4 1o(2 4)。

从以上我们可以获得，假如包括1，算法复杂度严苛为o (2 (n-1))。如果我们从N>1逐渐，算法复杂度为o (2 n)。斐波那契数列较长，N->∞，因此斐波那契数列的算法复杂度能够立即当做o (2 n)。

怎样看待阶乘算法复杂度O(n！)?

O(N!)

使我们改动上边的编码，并插入一个记数来记数O(n！)。

let count = 0;function nFacRuntimeFunc(n) { for(let i=0; i

阶乘种类O(n！)依据(n！ (n-1)！ (n-2)！ 1) ((n-1)！ (n-2)！ 1)来测算。哦，这也是多种阶乘的和。不仅是n * (n-1) * (n-2) * (n-3) 1。上例中的Count是复杂性的值。

n多次n！ (n-1)！ 1!countO(n！)111O(1)2(2！ 1!) (1!)4O(4)3(3！ (2! 1!) 1!) ((2! 1!) 1!) (1!)15O(15)4…64O(64)5…325 o(325)6…1956 o(1956)7…13699 o(13699)8…109600 o(109600)9…986409 o(986409)10…9864100 o(9864100)

迅速看这张表，当n为10时，O(n！)做到了O(9864100)，贴近O(干万)。这一优化算法的特性确实差到顶点。