本文由 发布,转载请注明出处,如有问题请联系我们! 发布时间: 2021-05-18Python数模笔记-NetworkX(2)最短路径
加载中Python数学模型手记-NetworkX(2)最短路径算法
1、最短路径算法难题的常用算法
最短路径算法难题是图论科学研究中的经典算法难题,用以计算图中一个端点到另一个端点的最短路径算法。
1.1 最短路径算法长短与最少权重计算途径长短
在日常日常生活,最短路径算法长短与最短路径算法间距仿佛并没有什么差别。但在实际的图论难题中却可能是不一样的定义和难题,常常会被搞混。
图论中有没有权利图和有权利图,没有权利图上的边沒有权,增权图的有边有权利,能够表明间距、時间、花费或其他指标值。在难题文字说明中,通常并不立即强调是没有权利图或是有权利图,这时候就需要留意最短路径算法与最少权重计算途径的差别。途径长短是把每一个端点到邻近端点的长短记为 1,而不是指这两个端点中间路面的间距——2个端点中间的路面间距是联接边的权(weight)。简单地说,途径长短能够觉得是飞行棋的计步,或是公交车站牌的站数,邻近端点中间为一步,间隔好多个端点便是几公里。途径长短是以途径起始点到终点站的计步,测算最短路径算法是要测算从起始点到终点站计步最少的途径。
假如难题不涉及到端点中间的间距,规定从起始点到终点站的最短路径算法及相匹配的最少长短,就是指从这一条线路从起始点到终点站有几公里,在图论中称之为最短路径算法长短。可是,假如难题得出端点中间的路面长短或间距,暂且称之为各界段的间距,规定从起始点到终点站的最短路径算法及相匹配的最短路线,显而易见并并不是在找历经至少计步的途径,只是在找途径中各界段的间距之和最少的途径,在图论中称之为最短权重计算途径长短——这儿权重值是道路间距。
=== 关心 Youcans 原創系列产品(https://www.cnblogs.com/youcans/)
1.2 最短路径算法的常用算法
求得最短路径算法长短的常用算法是 Dijkstra 优化算法、Bellman-Ford 优化算法和Floyd 优化算法,此外也有启发式算法 A*。
- Dijkstra 优化算法
Dijkstra 优化算法用以测算有权利图上最短路径算法难题 。该优化算法从起始点逐渐,选用贪婪法对策,每一次解析xml到起始点间距近期且未浏览过的端点的临接连接点, 直至拓展到终点站截止。
Dijkstra 优化算法的算法复杂度为 O(n^2)。假如边数远低于 n^2,可以用堆结构将复杂性降为O((m n)log(n))。
Dijkstar优化算法不可以解决负权边。
- Bellman-Ford 优化算法
Bellman-Ford 优化算法用以求得单源最短路径算法难题。优化算法基本原理是对图开展 V-1次松驰实际操作,获得全部很有可能的最短路径算法。
Bellman-Ford 优化算法的算法复杂度达到 O(V*E),V、E 分别是端点和边的总数。
Bellman-Ford 优化算法能够解决负权边。其操作过程“扩展”是在深层上检索,而“松驰”实际操作则在深度广度上检索,因而能够对负权边开展实际操作而不危害結果。
- Floyd 优化算法
Floyd 优化算法又被称为插点法,运用动态规划观念求得有权利图上多源点中间最短路径算法难题。优化算法从图的带权邻接矩阵逐渐,递归算法地开展 n 次升级获得图的间距引流矩阵,从而能够获得最短路径算法连接点引流矩阵。
Floyd 优化算法的算法复杂度为 O(n^3),空间复杂度为 O(n^2)。优化算法算法复杂度较高,不宜测算很多数据信息。Floyd 优化算法的优势是能够一次性求得随意2个连接点中间的最短路线,针对较密图的高效率高过实行 V 次 Dijkstra优化算法。
Floyd 优化算法能够解决负权边。
- A* 优化算法
A*优化算法是一种静态数据公路网中求得最短路径算法最有效的立即检索方式。
A*优化算法是启发式算法,选用最好是优先选择(Best-first)检索对策,根据定价涵数对每一个检索部位的评定結果,猜想最好是的部位优先选择开展检索。
A*优化算法巨大地降低了低品质的检索途径,因此检索高效率很高,比传统式的最短路径算法优化算法实用性高些、协调能力更强;可是,A*优化算法寻找的是相对性最佳途径,并不是肯定的最短路径算法,合适规模性、实用性高的难题。
1.3 最短路径算法优化算法的挑选
- 必须求得随意2个连接点中间的最短路线,应用 Floyd 优化算法;
- 只需求得单源最短路径算法难题,有负权边时应用 Bellman-Ford 优化算法,沒有负权边时应用 Dijkstra 优化算法;
- A*优化算法寻找的是相对性最佳途径,合适规模性、实用性高的难题。
2、NetworkX 中的最短路径算法优化算法
2.1 无向图和有向图的最短路径算法求得涵数
| 涵数 | 作用 |
|---|---|
| shortest_path(G[, source, target, weight,...]) | 计算图中的最短路径算法 |
| all_shortest_paths(G, source, target[,...]) | 计算图中全部最少的简易途径 |
| shortest_path_length(G[, source, target, ...]) | 计算图中的最短路径算法长短 |
| average_shortest_path_length(G[, weight, method]) | 测算均值最短路径算法长短 |
2.2 没有权利图最短路径算法优化算法
| 涵数 | 作用 |
|---|---|
| single_source_shortest_path(G, source[,cutoff]) | 测算从源到全部可以达到连接点的最短路径算法 |
| single_source_shortest_path_length(G,source) | 测算从源到全部可以达到连接点的最短路径算法长短 |
| single_target_shortest_path(G, target[,cutoff]) | 测算从全部可以达到连接点到总体目标的最短路径算法 |
| single_target_shortest_path_length(G,target) | 测算从全部可以达到连接点到总体目标的最短路径算法长短 |
| all_pairs_shortest_path(G[, cutoff]) | 测算全部连接点中间的最短路径算法 |
| all_pairs_shortest_path_length(G[, cutoff]) | 测算全部连接点中间的最短路径算法长短 |
2.3 有权利图最短路径算法优化算法
| 涵数 | 作用 |
|---|---|
| dijkstra_path(G, source, target[, weight]) | 测算从源到总体目标的最少权重计算途径 |
| dijkstra_path_length(G, source, target[,weight]) | 测算从源到总体目标的最少权重计算途径长短 |
| all_pairs_dijkstra_path(G[, cutoff, weight]) | 测算全部连接点中间的最少权重计算途径 |
| all_pairs_dijkstra_path_length(G[, cutoff,... ]) | 测算全部连接点中间的最少权重计算途径长短 |
| bellman_ford_path(G, source, target[, weight]) | 测算从源到总体目标的最短路径算法 |
| bellman_ford_path_length(G, source, target) | 测算从源到总体目标的最短路径算法长短 |
| all_pairs_bellman_ford_path(G[, weight]) | 测算全部连接点中间的最短路径算法 |
| all_pairs_bellman_ford_path_length(G[,weight]) | 测算全部连接点中间的最短路径算法长短 |
| floyd_warshall(G[, weight]) | 用 Floyd 法测算全部连接点中间的最短路径算法长短 |
| floyd_warshall_numpy(G[, nodelist, weight]) | 用 Floyd 法测算全部特定连接点中间的最短路径算法长短 |
3、NetworkX 中的 Dijkstra 优化算法
NetworkX 中有关 Dijkstra 优化算法给予了 13 个涵数,许多 涵数的作用是重合的。这儿只详细介绍最基本上的涵数 dijkstra_path() 和 dijkstra_path_length()。
3.1 dijkstra_path() 和 dijkstra_path_length() 使用说明书
dijkstra_path() 用以测算从源到总体目标的最少权重计算途径,dijkstra_path_length() 用以测算从源到总体目标的最少权重计算途径长短。
dijkstra_path(G, source, target, weight='weight')
dijkstra_path_length(G, source, target, weight='weight')
基本参数:
- G(NetworkX graph):图。
- source (node):起始点。
- target (node):终点站。
- weight (string or function):主要参数为字符串数组(string)时,按该字符串数组搜索边的特性做为权重值;假如该字符串数组相匹配的边特性不会有,则权重值置为1;主要参数为涵数时,边的权重值是涵数的传参。
传参:
dijkstra_path() 的传参是最短权重计算途径中的连接点目录,基本数据类型为list。
dijkstra_path_length() 的传参是最短权重计算途径的长短(途径中的边的权重值之和),基本数据类型为 number。
3.2 dijkstra_path() 优化算法应用方法
本实例难题来源于:司守奎、孙兆亮,数学模型优化算法与运用(第二版),P43,例4.3,国防科技出版社出版。
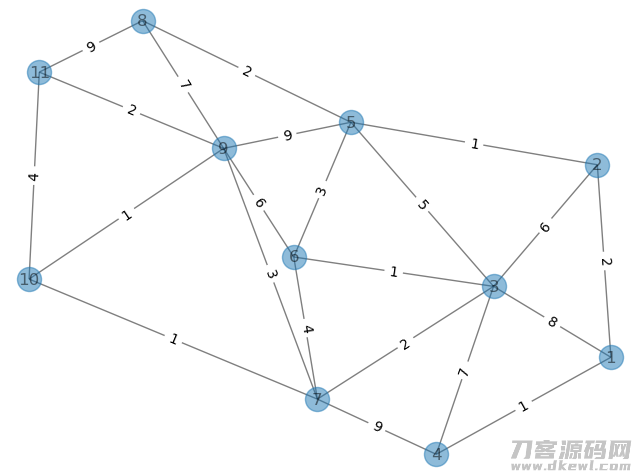
例4.3:无向图的最短路难题。已经知道如图所示的有权利无向图,求端点 v1 到 端点 v11 的最短路径算法。
# networkX_E2.py
# Demo of shortest path with NetworkX
# Copyright 2021 YouCans, XUPT
# Crated:2021-05-18
import matplotlib.pyplot as plt # 导进 Matplotlib 工具箱
import networkx as nx # 导进 NetworkX 工具箱
# 难题 2:无向图的最短路难题(司守奎,数学模型优化算法与运用,P43,例4.3)
G2 = nx.Graph() # 建立:空的 无向图
G2.add_weighted_edges_from([(1,2,2),(1,3,8),(1,4,1),
(2,3,6),(2,5,1),
(3,4,7),(3,5,5),(3,6,1),(3,7,2),
(4,7,9),
(5,6,3),(5,8,2),(5,9,9),
(6,7,4),(6,9,6),
(7,9,3),(7,10,1),
(8,9,7),(8,11,9),
(9,10,1),(9,11,2),
(10,11,4)]) # 向图上加上好几条增权边: (node1,node2,weight)
# 2个特定端点中间的最少权重计算途径
minWPath_v1_v11 = nx.dijkstra_path(G2, source=1, target=11) # 端点 0 到 端点 3 的最少权重计算途径
print("端点 v1 到 端点 v11 的最少权重计算途径: ", minWPath_v1_v11)
# 2个特定端点中间的最少权重计算途径的长短
lMinWPath_v1_v11 = nx.dijkstra_path_length(G2, source=1, target=11) #最短权重计算途径长短
print("端点 v1 到 端点 v11 的最少权重计算途径长短: ", lMinWPath_v1_v11)
# 关心 Youcans 原創系列产品(https://www.cnblogs.com/youcans/)
pos = nx.spring_layout(G2) # 用 FR优化算法排序连接点
nx.draw(G2, pos, with_labels=True, alpha=0.5)
labels = nx.get_edge_attributes(G2,'weight')
nx.draw_networkx_edge_labels(G2, pos, edge_labels = labels)
plt.show()
3.3 程序执行結果
端点 v1 到 端点 v11 的最少权重计算途径: [1, 2, 5, 6, 3, 7, 10, 9, 11]
端点 v1 到 端点 v11 的最少权重计算途径长短: 13
3.4 程序流程表明
- 图的键入。本例为稀少的有权利无向图,应用 G.add_weighted_edges_from() 涵数能够应用目录向图上加上好几条增权边,每一个增权边以元组 (node1,node2,weight) 表明。
- 图的制作。应用nx.draw()制图时,默认设置的连接点部位很有可能并不理想化,nx.spring_layout() 应用 Fruchterman-Reingold 力定项优化算法精准定位连接点。
- 制作边的特性。应用 nx.draw_networkx_edge_labels() 能够制作边的特性,方法中挑选表明权重值特性。
4、NetworkX 中的 Bellman-Ford 优化算法
NetworkX 中有关 Bellman-Ford 优化算法给予了 13 个涵数,许多 涵数的作用是重合的。这儿只详细介绍最基本上的涵数 bellman_ford_path() 和 bellman_ford_path_length()。
4.1 bellman_ford_path() 和 bellman_ford_path_length() 使用说明书
bellman_ford_path() 用以测算从源到总体目标的最少权重计算途径,bellman_ford_path_length() 用以测算从源到总体目标的最少权重计算途径长短。
bellman_ford_path(G, source, target, weight='weight')
bellman_ford_path_length(G, source, target, weight='weight')
基本参数:
- G(NetworkX graph):图。
- source (node):起始点。
- target (node):终点站。
- weight (string):按字符串数组搜索边的特性做为权重值。初始值为权重值 'weight'。
传参:
bellman_ford_path() 的传参是最短权重计算途径中的连接点目录,基本数据类型为list。
bellman_ford_path_length() 的传参是最短权重计算途径的长短(途径中的边的权重值之和),基本数据类型为 number。
4.2 bellman_ford_path() 优化算法应用方法
本实例难题来源于:司守奎、孙兆亮,数学模型优化算法与运用(第二版),P41,例4.1,国防科技出版社出版。
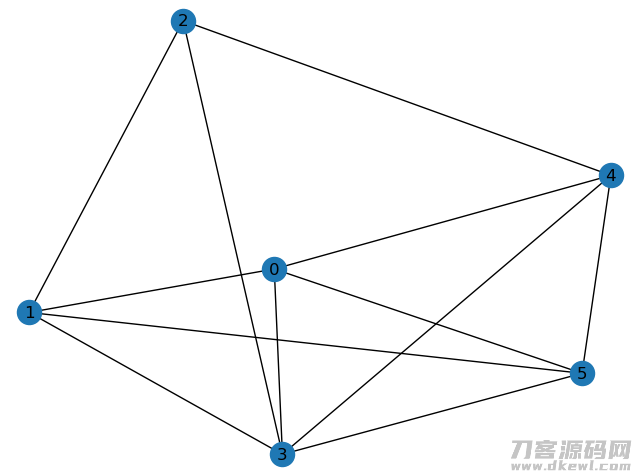
例4.1:大城市间机票价格难题。已经知道 6个城市的飞机票门票如引流矩阵所显示(无穷表明沒有直飞),求大城市 c1 到其他大城市 c2...c6 的门票最划算的途径及门票。
# networkX_E1.py
# Demo of shortest path with NetworkX
# Copyright 2021 YouCans, XUPT
# Crated:2021-05-18
import pandas as pd
import matplotlib.pyplot as plt # 导进 Matplotlib 工具箱
import networkx as nx # 导进 NetworkX 工具箱
# 难题 1:大城市间机票价格难题(司守奎,数学模型优化算法与运用,P41,例4.1)
# # 从Pandas数据类型(端点邻接矩阵)建立 NetworkX 图
# # from_pandas_adjacency(df, create_using=None) # 邻接矩阵,n行*n列,引流矩阵数指权重值
dfAdj = pd.DataFrame([[0, 50, 0, 40, 25, 10], # 0 表明不临接,
[50, 0, 15, 20, 0, 25],
[0, 15, 0, 10, 20, 0],
[40, 20, 10, 0, 10, 25],
[25, 0, 20, 10, 0 ,55],
[10, 25, 0, 25, 55, 0]])
G1 = nx.from_pandas_adjacency(dfAdj) # 由 pandas 端点邻接矩阵 建立 NetworkX 图
# 测算最短路径算法:留意最短路径算法与最少权重计算途径的不一样
# 2个特定端点中间的最短路径算法
minPath03 = nx.shortest_path(G1, source=0, target=3) # 端点 0 到 端点 3 的最短路径算法
lMinPath03 = nx.shortest_path_length(G1, source=0, target=3) #最短路径算法长短
print("端点 0 到 3 的最短路径算法为:{},最短路径算法长短为:{}".format(minPath03, lMinPath03))
# 2个特定端点中间的最少权重计算途径
minWPath03 = nx.bellman_ford_path(G1, source=0, target=3) # 端点 0 到 端点 3 的最少权重计算途径
# 2个特定端点中间的最少权重计算途径的长短
lMinWPath03 = nx.bellman_ford_path_length(G1, source=0, target=3) #最短权重计算途径长短
print("端点 0 到 3 的最少权重计算途径为:{},最短权重计算途径长短为:{}".format(minWPath03, lMinWPath03))
for i in range(1,6):
minWPath0 = nx.dijkstra_path(G1, source=0, target=i) # 端点 0 到其他端点的最少权重计算途径
lMinPath0 = nx.dijkstra_path_length(G1, source=0, target=i) #最短权重计算途径长短
print("大城市 0 到 大城市 {} 飞机票门票最少的线路为: {},门票总数为:{}".format(i, minWPath0, lMinPath0))
# # 关心 Youcans 原創系列产品(https://www.cnblogs.com/youcans/)
# nx.draw_networkx(G1) # 默认设置带外框,端点标识
nx.draw(G1, with_labels=True, layout=nx.spring_layout(G1))
plt.show()
4.3 程序执行結果
端点 0 到 3 的最短路径算法为:[0, 3],最短路径算法长短为:1
端点 0 到 3 的最少权重计算途径为:[0, 4, 3],最短权重计算途径长短为:35
大城市 0 到 大城市 1 飞机票门票最少的线路为: [0, 5, 1],门票总数为:35
大城市 0 到 大城市 2 飞机票门票最少的线路为: [0, 4, 2],门票总数为:45
大城市 0 到 大城市 3 飞机票门票最少的线路为: [0, 5, 3],门票总数为:35
大城市 0 到 大城市 4 飞机票门票最少的线路为: [0, 4],门票总数为:25
大城市 0 到 大城市 5 飞机票门票最少的线路为: [0, 5],门票总数为:10
4.4 程序流程表明
- 图的键入。应用 pandas 中 DataFrame 获取数据文档十分便捷,本例中以 pandas 键入端点邻接矩阵,应用 nx.from_pandas_adjacency(dfAdj) 变换为 NetworkX 的图。
- 邻接矩阵。邻接矩阵 dfAdj (i,j) 的值表明联接端点 i、j 的边的权重值, i、j 不邻近 dfAdj (i,j) =0, 本例中表明沒有直飞。
- 最短路径算法与最短路径算法长短。nx.shortest_path() 回到最短路径算法。nx.shortest_path_length() 回到最短路径算法长短,本例中能够了解为从起始点到终点站的乘飞机频次,1 表明直飞,2 表明转站一次。
- 最短权重计算途径长短。nx.bellman_ford_path_length() 回到最短权重计算途径长短,本例中权重值为门票,最短权重计算途径长短即是二点间最划算的直飞或转站的飞机票门票。
根据本实例,能够形象化地了解最短路径算法长短与最少权重计算途径长短的差别。
关心 Youcans 原創系列产品(https://www.cnblogs.com/youcans/)===
著作权表明:
文中內容及方法为创作者原創,并不是转截书本或互联网內容。
文中中实例难题来源于:
1、司守奎、孙兆亮,数学模型优化算法与运用(第二版),国防科技出版社出版。
YouCans 原创作品
Copyright 2021 YouCans, XUPT
Crated:2021-05-18









